(以“分类:整数处理 ==摘要== {{信息题|Vasily the Bear and Fly|http://acm.hust.edu.cn/vjudge/contest/view.action?cid{{=}}70748#problem/G|1|100|输出顺序|1...”为内容创建页面) |
小 (补充) |
||
| 第1行: | 第1行: | ||
[[分类:整数处理]] | [[分类:整数处理]] | ||
==摘要== | ==摘要== | ||
| − | {{信息题|Vasily the Bear and Fly|http://acm.hust.edu.cn/vjudge/contest/view.action?cid{{=}}70748#problem/G|1|100| | + | {{信息题|Vasily the Bear and Fly|http://acm.hust.edu.cn/vjudge/contest/view.action?cid{{=}}70748#problem/G|1|100|遗漏情况|1|time=2015-02-27 12:35:20}} |
*来自寒假练习:[http://acm.hust.edu.cn/vjudge/contest/view.action?cid=70748 2015 Winter Day 4 div1] G题 | *来自寒假练习:[http://acm.hust.edu.cn/vjudge/contest/view.action?cid=70748 2015 Winter Day 4 div1] G题 | ||
*原题链接:http://codeforces.com/problemset/problem/336/B | *原题链接:http://codeforces.com/problemset/problem/336/B | ||
==题意== | ==题意== | ||
| − | 坐标轴上有2*n个R为半径两两相邻的圆,问任取圆心第(1,i)和(2,j)<small>(i,j表示序号而非坐标)</small> | + | 坐标轴上有2*n个R为半径两两相邻的圆,问任取圆心第(1,i)和(2,j)<small>(i,j表示序号而非坐标)</small>之间的最短路径的数学期望(路径要求都在圆内)。 |
==题解== | ==题解== | ||
*理解了题意确实做起来不是太难,肯定不能暴力,要优化到O(n)。 | *理解了题意确实做起来不是太难,肯定不能暴力,要优化到O(n)。 | ||
| 题目链接 | 难度等级 | 完成状态 | 完成分数 | 最后编辑时间 | 失误原因(初次提交分数) |
|---|---|---|---|---|---|
| Vasily the Bear and Fly | ★☆☆☆☆ | 答案正确 | 100 | 2015-02-27 12:35:20 | 遗漏情况(1) |
坐标轴上有2*n个R为半径两两相邻的圆,问任取圆心第(1,i)和(2,j)(i,j表示序号而非坐标)之间的最短路径的数学期望(路径要求都在圆内)。
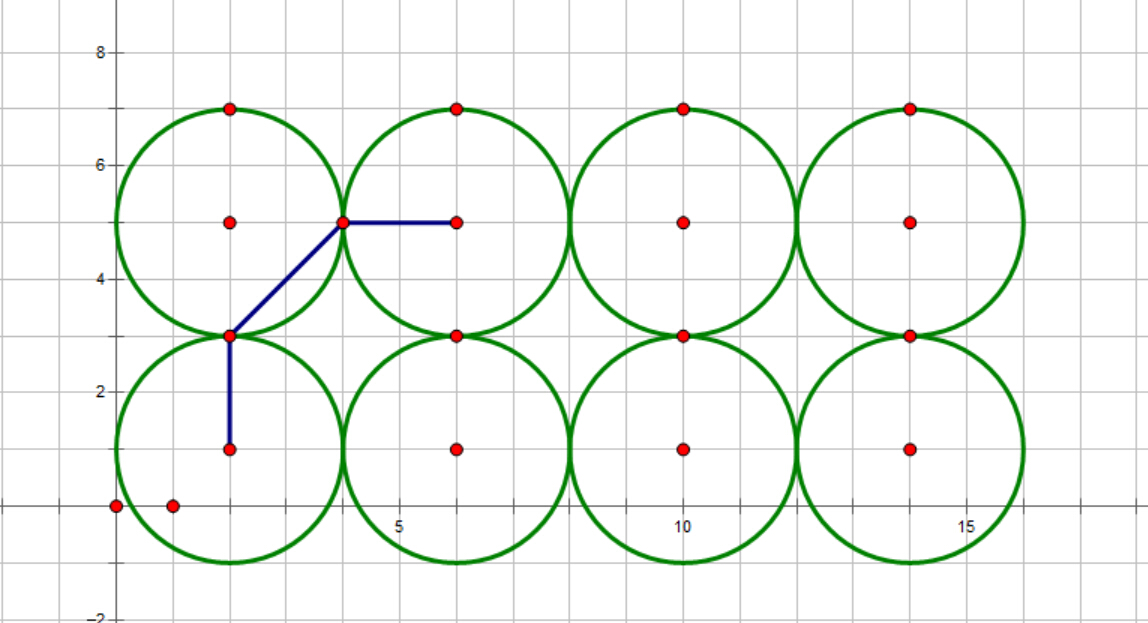
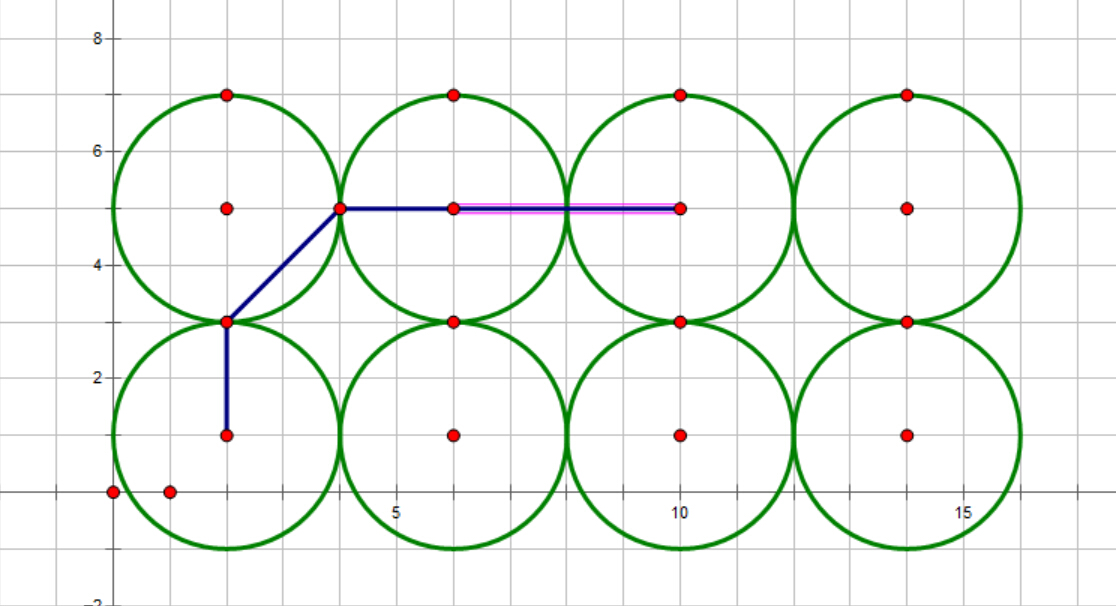
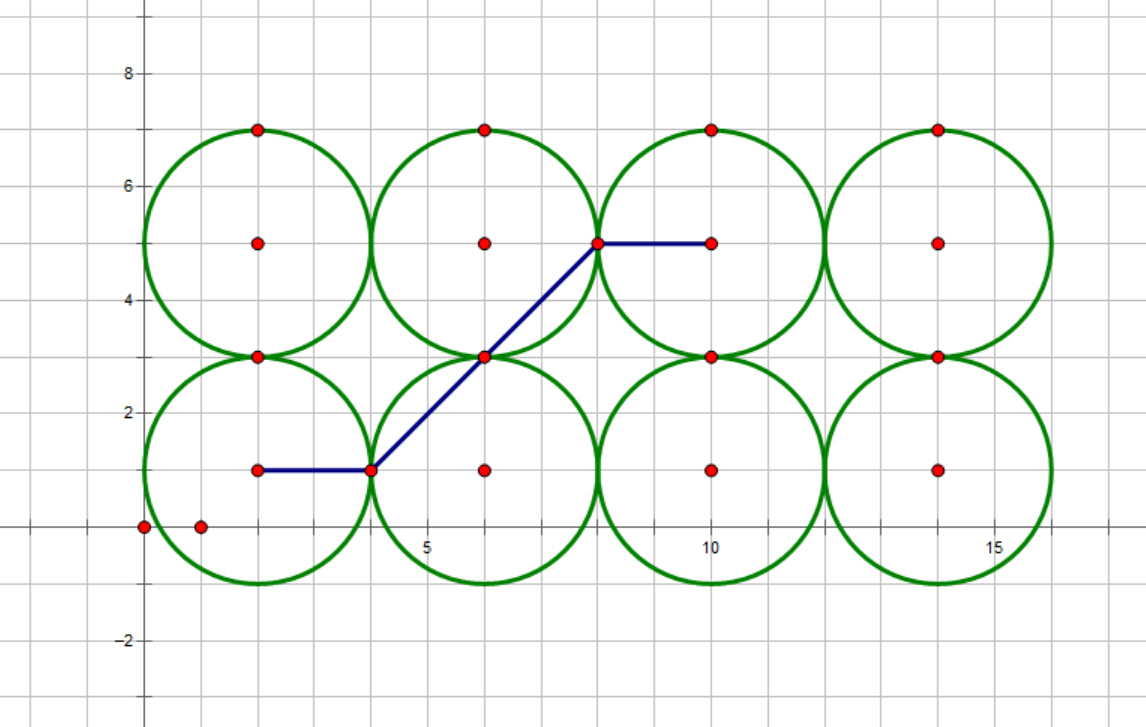
扯个题外话:java里BigDecimal的divide要求第二个参数是精度,不要漏了- -
| 336B.java代码已折叠
展开折叠内容
|
|---|
import java.io.BufferedInputStream;
import java.math.BigDecimal;
import java.math.RoundingMode;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner cin = new Scanner(new BufferedInputStream(System.in));
int m = cin.nextInt();
BigDecimal R = cin.nextBigDecimal();
BigDecimal ans = BigDecimal.ZERO, TWO = BigDecimal.valueOf(2), s2 = new BigDecimal(
Math.sqrt(2));
for (int i = 0; i != m; ++i) {
BigDecimal v = BigDecimal.ONE;
BigDecimal u = BigDecimal.valueOf(i);
u = u.add(BigDecimal.ONE);
BigDecimal dis = BigDecimal.ZERO;
if (u == v)
dis = R.multiply(TWO);// 2R//
else if (i == 1)
dis = R.multiply(BigDecimal.valueOf(i * 2)).add(s2.multiply(R));// 2iR+R//
else
dis = R.multiply(BigDecimal.valueOf(i * 2 - 2)).add(
s2.multiply(R.multiply(TWO)));// 2iR+R//
if (i != 0)
ans = ans.add(dis.multiply(BigDecimal.valueOf((m - i) * 2)));
else
ans = ans.add(dis.multiply(BigDecimal.valueOf(m - i)));
}
ans = ans.divide(BigDecimal.valueOf(m), 1000, RoundingMode.HALF_DOWN);
ans = ans.divide(BigDecimal.valueOf(m), 50, RoundingMode.HALF_DOWN);
System.out.println(ans);
return;
}
}
|